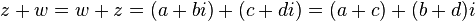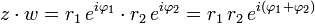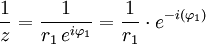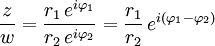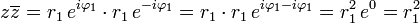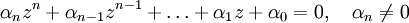Fotos:
quarta-feira, 28 de setembro de 2011
Metrópole: da língua grega metropolis (μήτηρ, mētēr = mãe, ventre e πόλις, pólis = cidade), é o termo empregado para se designar as cidades centrais de áreas urbanas formadas por cidades ligadas entre si fisicamente (conurbadas)[2][3] ou através de fluxos de pessoas e serviços[2] ou que assumem importante posição (econômica, política, cultural, etc.) na rede urbana da qual fazem parte (correspondentes, na classificação do IBGE,[2] às metrópoles nacionais e regionais).
Fotos:
Fotos:
segunda-feira, 12 de setembro de 2011
Trabalho de Matemática (Profº Alberto) - Pollyana Calves, Priscila Gabrielle e João Guilherme.
Johann Carl Friedrich Gauss (ou Gauß) Conhecido como o príncipe dos matemáticos, muitos o consideram o maior gênio da história da matemática. Seu QI foi estimado por psicólogos de cognição em cerca de 240.



Seu pai, Gerhard Diederich, era jardineiro e pedreiro. Severo e brutal, tudo fez para impedir que seu filho desenvolvesse seu grande potencial. Foi salvo por sua mãe Dorothea e seu tio Friederich que percebeu da inteligência de seu sobrinho.
Tinha memória fotográfica, tendo retido as impressões da infância e da meninice nítidas até a sua morte. Ressentia-se de que seu tio Friederich, um gênio, perdera-se pela morte prematura.
Antes disso já aprendera a ler e a somar sozinho. Aos sete anos entrou para a escola. Segundo uma história famosa, seu diretor, Butner, pediu que os alunos somassem os números inteiros de um a cem. Mal havia enunciado o problema e o jovem Gauss colocou sua lousa sobre a mesa, dizendo: ligget se! Sua resposta, 5050, foi encontrada através do raciocínio que demonstra a fórmula da soma de uma progressão aritmética. Alguns autores argumentam que o problema seria de ordem bastante mais complexa, sugerindo que poderia ser uma soma de uma progressão aritmética como 81097 + 81395 + 81693 + ..... + 110897.Butner ficou tão atônito com a proeza de um menino de dez anos que pagou do próprio bolso livros de aritmética para ele, que os absorvia instantaneamente. Reconhecendo que fora ultrapassado pelo aluno, passou o ensino para seu jovem assistente, Johann Martin Bartels (1769-1856), apaixonado pela matemática. Entre Bartels, com dezessete anos, e o aluno de dez nasceu uma boa amizade que durou toda a vida. Eles estudavam juntos, ajudando-se em suas dificuldades.
O encontro de Gauss com o teorema binômio inspirou-o para alguns de seus maiores trabalhos, tornando-se Gauss o primeiro "rigorista". Insatisfeito com o que ele e Bartels encontravam em seus livros, Gauss foi além, e iniciou a análise matemática.
Nenhum matemático anterior tinha a menor concepção do que é agora aceitável como prova, envolvendo o processo infinito. Ele foi o primeiro a ver que, a "prova" que pode levar a absurdos como "menos 1 é igual ao infinito", não é prova nenhuma. Mesmo que, em alguns casos, uma fórmula dê resultados consistentes, ela não tem lugar na matemática até que a precisa condição sob a qual ela continuará a se submeter tenha sido determinada consistentemente. O rigor imposto por Gauss à análise matemática tornou-a totalmente diferente e superou toda a análise matemática feita por seus antecessores.
Jean Robert Argand nasceu em Genebra (Suiça), a 18 de Julho de 1768. Apesar de ser apenas um matemático amador, Argand ficou famoso pela sua interpretação geométrica dos números complexos, onde i é interpretado como uma rotação de 90º.
O primeiro a publicar a interpretação geométrica de Argand foi Caspar Wessel, no entanto, o nome de Argand nunca apareceu no livro, e por isso era impossível identificar o seu autor. Foi necessário muito tempo para que o trabalho de Argand fosse conhecido como seu.
Em Setembro de 1813, Jacques Français publicou um trabalho no qual aparecia uma representação geométrica dos números complexos, com aplicações interessantes, baseadas nas ideias de Argand. Nesta publicação, Jacques Français dizia que as ideias eram baseadas no trabalho de um matemático desconhecido, e pedia que este se desse a conhecer, para receber o devido crédito pelas suas ideias. O artigo apareceu no jornal GergonneŽs, e Argand respondeu a Jacques Français dizendo que era ele o autor dessas ideias. A partir daqui o trabalho de Argand começou a ser conhecido.
Argand apresentou ainda uma prova para o "Teorema Fundamental da Álgebra", sendo, possivelmente, o primeiro a trabalhar com o teorema no caso em que os coeficientes são números complexos.
Jean Robert Argand faleceu a 13 de Agosto de 1822, em Paris.
Plano de Argand-Gauss:
A cada número complexo z = a + bi, podemos associar um ponto P no plano cartesiano. No complexo podemos representar a parte real por um ponto no eixo real, e a parte imaginária por um ponto no eixo vertical, denominado eixo imaginário.
A este ponto P, correspondente ao complexo z = a +bi, chamamos de imagem ou afixo de z. Observe a representação da interpretação geométrica dos números complexos:

A este ponto P, correspondente ao complexo z = a +bi, chamamos de imagem ou afixo de z. Observe a representação da interpretação geométrica dos números complexos:

Atualmente, o plano dos números complexos é conhecido como plano de Argand-Gauss.
Com base no plano representado vamos calcular a distância p (letra grega: rô), entre os pontos O e P. Observe que basta aplicarmos o Teorema de Pitágoras no triângulo retângulo, dessa forma temos:
Com base no plano representado vamos calcular a distância p (letra grega: rô), entre os pontos O e P. Observe que basta aplicarmos o Teorema de Pitágoras no triângulo retângulo, dessa forma temos:
O módulo de z é representado pela grandeza p, mas também pode ser representado por |z|.
A ângulo Ө (0 ≤ Ө < 2π), formado pelo eixo real e a reta do segmento OP, é chamado de argumento de z (z ≠ 0) e é indicado por Arg(z). Baseado nessas definições podemos estabelecer as seguintes relações na interpretação geométrica dos complexos:

A ângulo Ө (0 ≤ Ө < 2π), formado pelo eixo real e a reta do segmento OP, é chamado de argumento de z (z ≠ 0) e é indicado por Arg(z). Baseado nessas definições podemos estabelecer as seguintes relações na interpretação geométrica dos complexos:

Exemplo
Calcule o módulo e o argumento do número complexo z = 1 + 2i.
Módulo
a = 1 e b = 2

Argumento
Ө = Arg(z)
Calcule o módulo e o argumento do número complexo z = 1 + 2i.
Módulo
a = 1 e b = 2

Argumento
Ө = Arg(z)

Portanto, o argumento de z é o arco cuja tangente é 2.
Veja como ficaria o gráfico representativo do número complexo z = 1 + 2i.

quinta-feira, 8 de setembro de 2011
História dos Números Complexos
O fato de um número negativo não ter raiz quadrada parece ter sido sempre claro para os matemáticos que se depararam com essa questão. Um número complexo é um número z que pode ser escrito na forma z = x + iy, em que x e y são números reais e i denota a unidade imaginária. Esta tem a propriedade i2 = − 1. Onde x e y são chamados respectivamente parte real e parte imaginária de z.[1] O conjunto dos números complexos, denotado por  , contém o conjunto dos números reais. Munido de operações de adição e multiplicação obtidas por extensão das operações de adição e multiplicação nos reais, adquire uma estrutura algébrica denominada corpo. Esse corpo é algebricamente fechado, isto é, contém todas as soluções de quaisquer equações polinomiais com coeficientes complexos. O conjunto dos números complexos também pode ser visto como um espaço vetorial, tanto sobre
, contém o conjunto dos números reais. Munido de operações de adição e multiplicação obtidas por extensão das operações de adição e multiplicação nos reais, adquire uma estrutura algébrica denominada corpo. Esse corpo é algebricamente fechado, isto é, contém todas as soluções de quaisquer equações polinomiais com coeficientes complexos. O conjunto dos números complexos também pode ser visto como um espaço vetorial, tanto sobre  como sobre
como sobre  .
.
Além disso, a cada número complexo podemos atribuir um número real positivo chamado módulo, dado por:
Os números complexos são representados geometricamente no plano complexo. Nele, representa-se a parte real, x, no eixo horizontal e a parte imaginária, y, no eixo vertical.
Os números complexos são utilizados em várias áreas do conhecimento, tais como engenharia, eletromagnetismo, física quântica, teoria do caos, além da própria matemática, em que são estudadas análise complexa, álgebra linear complexa, álgebra de Lie complexa, com aplicações em resolução de equações algébricas e equações diferenciais.
Em engenharia e física, é comum a troca da letra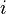 pela letra
pela letra  , devido ao freqüente uso da primeira como indicação de corrente elétrica.
, devido ao freqüente uso da primeira como indicação de corrente elétrica.
Os primeiros que conseguiram dar soluções a equações cúbicas foram Scipione del Ferro e Tartaglia. Este último, depois de ter sido alvo de muita insistência, passou os resultados que tinha obtido a Girolamo Cardano, que prometeu não divulgá-los. Cardano, depois de conferir a exatidão das resoluções de Tartaglia, não honrou sua promessa e publicou os resultados, mencionando o autor, em sua obra Ars Magna de 1545, iniciando uma enorme inimizade.
A fórmula deduzida por Tartaglia afirmava que a solução da equação x3 + px + q = 0 era dada por
Por exemplo, a equação:
tem três raízes reais, como se pode observar facilmente ou pelo gráfico da função:
Entretanto, usando-se a fórmula de Tartaglia, chega-se a:
Rafael Bombelli experimentou escrever as expressões:
Abraham de Moivre e Euler, no século XVIII começaram a estabelecer uma estrutura algébrica para os números complexos. Em particular, Euler denotou a raiz quadrada de -1 por i. Ainda no século XVIII os números complexos passaram a ser interpretados como pontos do plano (plano de Argand-Gauss), o que permitiu a escrita de um número complexo na forma polar. Com isso, conseguiu-se calcular potências e raízes de modo eficiente e claro. Ainda no século XVIII, Gauss demonstrou o Teorema Fundamental da Álgebra.
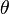 é o ângulo entre a semi-reta
é o ângulo entre a semi-reta 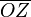 e o semi-eixo real, chamado de argumento do número complexo Z e denotado por
e o semi-eixo real, chamado de argumento do número complexo Z e denotado por  .
.
Através da identidade , a forma polar é equivalente à chamada forma exponencial:
, a forma polar é equivalente à chamada forma exponencial: 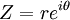

Sejam z e w dois números complexos dados por e
e  então definem-se as relações e operações elementares tal como segue:
então definem-se as relações e operações elementares tal como segue:
 e
e  , o módulo possui as seguintes propriedades:
, o módulo possui as seguintes propriedades:
Este resultado é conhecido como teorema fundamental da álgebra e foi demonstrado primeiramente pelo matemático alemão Carl Friedrich Gauss. Uma consequência deste teorema é que todo polinômio de grau n pode ser decomposto em um produto de n fatores lineares complexos:
 , que são dadas pela fórmula de De Moivre:
, que são dadas pela fórmula de De Moivre:
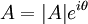 .
.
 forma um espaço métrico completo. De fato, o módulo possui todas as características de uma norma.
forma um espaço métrico completo. De fato, o módulo possui todas as características de uma norma.
 de números complexos é convergente se existe um número complexo
de números complexos é convergente se existe um número complexo 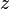 tal que:
tal que:
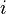 pode ser interpretado como o elemento que gera a extensão algébrica dos números reais contendo a raiz do polinômio
pode ser interpretado como o elemento que gera a extensão algébrica dos números reais contendo a raiz do polinômio  . Isto é, o corpo
. Isto é, o corpo  é isomorfo ao corpo quociente
é isomorfo ao corpo quociente  pela aplicação
pela aplicação  , homomorfismo de anéis tal que restrito aos reais é a aplicação identidade e que leva
, homomorfismo de anéis tal que restrito aos reais é a aplicação identidade e que leva 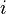 em
em  .
.
 , contém o conjunto dos números reais. Munido de operações de adição e multiplicação obtidas por extensão das operações de adição e multiplicação nos reais, adquire uma estrutura algébrica denominada corpo. Esse corpo é algebricamente fechado, isto é, contém todas as soluções de quaisquer equações polinomiais com coeficientes complexos. O conjunto dos números complexos também pode ser visto como um espaço vetorial, tanto sobre
, contém o conjunto dos números reais. Munido de operações de adição e multiplicação obtidas por extensão das operações de adição e multiplicação nos reais, adquire uma estrutura algébrica denominada corpo. Esse corpo é algebricamente fechado, isto é, contém todas as soluções de quaisquer equações polinomiais com coeficientes complexos. O conjunto dos números complexos também pode ser visto como um espaço vetorial, tanto sobre  como sobre
como sobre  .
.Além disso, a cada número complexo podemos atribuir um número real positivo chamado módulo, dado por:
 .
.
Os números complexos são representados geometricamente no plano complexo. Nele, representa-se a parte real, x, no eixo horizontal e a parte imaginária, y, no eixo vertical.
Os números complexos são utilizados em várias áreas do conhecimento, tais como engenharia, eletromagnetismo, física quântica, teoria do caos, além da própria matemática, em que são estudadas análise complexa, álgebra linear complexa, álgebra de Lie complexa, com aplicações em resolução de equações algébricas e equações diferenciais.
Em engenharia e física, é comum a troca da letra
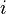 pela letra
pela letra  , devido ao freqüente uso da primeira como indicação de corrente elétrica.
, devido ao freqüente uso da primeira como indicação de corrente elétrica.História
O conceito de número complexo teve um desenvolvimento gradual. Começaram a ser utilizados formalmente no século XVI em fórmulas de resolução de equações de terceiro e quarto graus.Os primeiros que conseguiram dar soluções a equações cúbicas foram Scipione del Ferro e Tartaglia. Este último, depois de ter sido alvo de muita insistência, passou os resultados que tinha obtido a Girolamo Cardano, que prometeu não divulgá-los. Cardano, depois de conferir a exatidão das resoluções de Tartaglia, não honrou sua promessa e publicou os resultados, mencionando o autor, em sua obra Ars Magna de 1545, iniciando uma enorme inimizade.
A fórmula deduzida por Tartaglia afirmava que a solução da equação x3 + px + q = 0 era dada por
Por exemplo, a equação:
- x3 − 15x − 4 = 0
tem três raízes reais, como se pode observar facilmente ou pelo gráfico da função:
- f(x) = x3 − 15x − 4
- x3 − 15x − 4 = (x − 4)(x2 + 4x + 1) = 0
 ;
; ;
;
 .
.
Entretanto, usando-se a fórmula de Tartaglia, chega-se a:
Rafael Bombelli experimentou escrever as expressões:
![\sqrt[3]{2+\sqrt{-121}}](http://upload.wikimedia.org/math/c/c/9/cc90d001e30dab0d17ca4df66fb7c438.png) e
e ![\sqrt[3]{2-\sqrt{-121}}](http://upload.wikimedia.org/math/c/e/f/ceff1f378ecad6c05acacfe87aea33a9.png)
 e
e 
Abraham de Moivre e Euler, no século XVIII começaram a estabelecer uma estrutura algébrica para os números complexos. Em particular, Euler denotou a raiz quadrada de -1 por i. Ainda no século XVIII os números complexos passaram a ser interpretados como pontos do plano (plano de Argand-Gauss), o que permitiu a escrita de um número complexo na forma polar. Com isso, conseguiu-se calcular potências e raízes de modo eficiente e claro. Ainda no século XVIII, Gauss demonstrou o Teorema Fundamental da Álgebra.
Plano complexo:
O plano complexo, também chamado de plano de Argand-Gauss é uma representação geométrica do conjunto dos números complexos. Da mesma forma como a cada ponto da reta está associado um número real, o plano complexo associa biunivocamente o ponto ( x , y ) do plano ao número complexo x + yi. Esta associação conduz a pelo menos duas formas de representar um número complexo:- Forma retangular ou cartesiana:
- Forma polar:
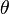 é o ângulo entre a semi-reta
é o ângulo entre a semi-reta 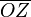 e o semi-eixo real, chamado de argumento do número complexo Z e denotado por
e o semi-eixo real, chamado de argumento do número complexo Z e denotado por  .
.Através da identidade
 , a forma polar é equivalente à chamada forma exponencial:
, a forma polar é equivalente à chamada forma exponencial: 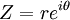
Operações elementares:
O conjunto dos números complexos é um corpo. Portanto, é fechado sobre as operações de adição e multiplicação, além de possuir a propriedade de que todo elemento não-nulo do conjunto possui um inverso multiplicativo. Todas as operações do corpo podem ser performadas através das propriedades associativa, comutativa e distributiva, levando em consideração a identidade
Sejam z e w dois números complexos dados por
 e
e  então definem-se as relações e operações elementares tal como segue:
então definem-se as relações e operações elementares tal como segue:- Identidade:
 se e somente se
se e somente se  e
e 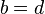 .
.
- Soma:
- Produto:
- Conjugado:
 , onde
, onde  denota o conjugado de z. Outra notação usada para o conjugado de z é z * .
denota o conjugado de z. Outra notação usada para o conjugado de z é z * .
- Produto de um Complexo por seu Conjugado:
 . Como i2 = − 1, temos que o produto de um Número Complexo a + bi pelo seu Conjugado a − bi se dá por:
. Como i2 = − 1, temos que o produto de um Número Complexo a + bi pelo seu Conjugado a − bi se dá por:  .
.
- Módulo:
- Inverso multiplicativo (para
 ):
):
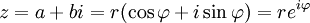 .
.
- Produto:
- Inverso multiplicativo (para
 ):
):
- Divisão:
- Potenciação:
- Conjugado:
O módulo:
Sejam z e w dois números complexos dados por e
e  , o módulo possui as seguintes propriedades:
, o módulo possui as seguintes propriedades:Propriedades algébricas:
O conjunto dos números complexos formam um corpo algebricamente fechado. Isso significa que toda equação algébrica de grau não nulo pode possuir como solução um número complexo. Mais formalmente, a seguinte equaçãoEste resultado é conhecido como teorema fundamental da álgebra e foi demonstrado primeiramente pelo matemático alemão Carl Friedrich Gauss. Uma consequência deste teorema é que todo polinômio de grau n pode ser decomposto em um produto de n fatores lineares complexos:
Radical algébrico
O radical algébrico é definido no conjunto dos números complexos como uma função multivalente, devido ao fato que a equação algébrica: , que são dadas pela fórmula de De Moivre:
, que são dadas pela fórmula de De Moivre: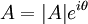 .
.Propriedades topológicas e analíticas
O conjunto dos números complexos munido da distância forma um espaço métrico completo. De fato, o módulo possui todas as características de uma norma.
forma um espaço métrico completo. De fato, o módulo possui todas as características de uma norma.Convergência nos complexos
Diz-se que uma sequência de números complexos é convergente se existe um número complexo
de números complexos é convergente se existe um número complexo 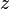 tal que:
tal que:- É fácil verificar que se
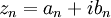 , então
, então  converge para
converge para 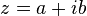 se e somente se
se e somente se 
 e
e  converge para
converge para 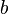 . converge para
. converge para - Do fato de que
 , é válido que se
, é válido que se  então
então 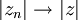
O conjunto dos números complexos como extensão algébrica
No campo da álgebra abstrata, o número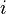 pode ser interpretado como o elemento que gera a extensão algébrica dos números reais contendo a raiz do polinômio
pode ser interpretado como o elemento que gera a extensão algébrica dos números reais contendo a raiz do polinômio  . Isto é, o corpo
. Isto é, o corpo  é isomorfo ao corpo quociente
é isomorfo ao corpo quociente  pela aplicação
pela aplicação  , homomorfismo de anéis tal que restrito aos reais é a aplicação identidade e que leva
, homomorfismo de anéis tal que restrito aos reais é a aplicação identidade e que leva 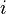 em
em  .
.Logaritmos
Função logarítmica natural
Definimos a função logarítmica natural de uma variável complexa z pela equação: =
=  +
+ 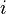 (
( 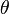 ±
±  )
)
 +
+ 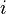
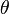
Função logarítmica decimal
Em termos de logaritmos decimais, podemos definir a função logarítmica anterior como:
 (
( 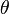 ±
±  )
)
Assinar:
Comentários (Atom)

![x = \sqrt[3]{-\frac{q}{2} + \sqrt{(\frac{q}{2})^2 +
(\frac{p}{3})^3}} + \sqrt[3]{- \frac{q}{2} - \sqrt{(\frac{q}{2})^2 +
(\frac{p}{3})^3}}.](http://upload.wikimedia.org/math/d/4/0/d40a53f0a19c385963fe4a7e455b725b.png)
![x=\sqrt[3]{2+\sqrt{-121}} + \sqrt[3]{2-\sqrt{-121}}](http://upload.wikimedia.org/math/7/d/5/7d5c0b00ec1dfa452318a220b4444549.png)
![x=\sqrt[3]{2+\sqrt{-121}} + \sqrt[3]{2-\sqrt{-121}} = (2 + \sqrt{-1}) + (2 - \sqrt{-1}) = 4](http://upload.wikimedia.org/math/4/9/e/49eaada2392d4bb6a501a76c68ff1a6c.png)