 , contém o conjunto dos números reais. Munido de operações de adição e multiplicação obtidas por extensão das operações de adição e multiplicação nos reais, adquire uma estrutura algébrica denominada corpo. Esse corpo é algebricamente fechado, isto é, contém todas as soluções de quaisquer equações polinomiais com coeficientes complexos. O conjunto dos números complexos também pode ser visto como um espaço vetorial, tanto sobre
, contém o conjunto dos números reais. Munido de operações de adição e multiplicação obtidas por extensão das operações de adição e multiplicação nos reais, adquire uma estrutura algébrica denominada corpo. Esse corpo é algebricamente fechado, isto é, contém todas as soluções de quaisquer equações polinomiais com coeficientes complexos. O conjunto dos números complexos também pode ser visto como um espaço vetorial, tanto sobre  como sobre
como sobre  .
.Além disso, a cada número complexo podemos atribuir um número real positivo chamado módulo, dado por:
 .
.
Os números complexos são representados geometricamente no plano complexo. Nele, representa-se a parte real, x, no eixo horizontal e a parte imaginária, y, no eixo vertical.
Os números complexos são utilizados em várias áreas do conhecimento, tais como engenharia, eletromagnetismo, física quântica, teoria do caos, além da própria matemática, em que são estudadas análise complexa, álgebra linear complexa, álgebra de Lie complexa, com aplicações em resolução de equações algébricas e equações diferenciais.
Em engenharia e física, é comum a troca da letra
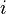 pela letra
pela letra  , devido ao freqüente uso da primeira como indicação de corrente elétrica.
, devido ao freqüente uso da primeira como indicação de corrente elétrica.História
O conceito de número complexo teve um desenvolvimento gradual. Começaram a ser utilizados formalmente no século XVI em fórmulas de resolução de equações de terceiro e quarto graus.Os primeiros que conseguiram dar soluções a equações cúbicas foram Scipione del Ferro e Tartaglia. Este último, depois de ter sido alvo de muita insistência, passou os resultados que tinha obtido a Girolamo Cardano, que prometeu não divulgá-los. Cardano, depois de conferir a exatidão das resoluções de Tartaglia, não honrou sua promessa e publicou os resultados, mencionando o autor, em sua obra Ars Magna de 1545, iniciando uma enorme inimizade.
A fórmula deduzida por Tartaglia afirmava que a solução da equação x3 + px + q = 0 era dada por
Por exemplo, a equação:
- x3 − 15x − 4 = 0
tem três raízes reais, como se pode observar facilmente ou pelo gráfico da função:
- f(x) = x3 − 15x − 4
- x3 − 15x − 4 = (x − 4)(x2 + 4x + 1) = 0
 ;
; ;
;
 .
.
Entretanto, usando-se a fórmula de Tartaglia, chega-se a:
Rafael Bombelli experimentou escrever as expressões:
![\sqrt[3]{2+\sqrt{-121}}](http://upload.wikimedia.org/math/c/c/9/cc90d001e30dab0d17ca4df66fb7c438.png) e
e ![\sqrt[3]{2-\sqrt{-121}}](http://upload.wikimedia.org/math/c/e/f/ceff1f378ecad6c05acacfe87aea33a9.png)
 e
e 
Abraham de Moivre e Euler, no século XVIII começaram a estabelecer uma estrutura algébrica para os números complexos. Em particular, Euler denotou a raiz quadrada de -1 por i. Ainda no século XVIII os números complexos passaram a ser interpretados como pontos do plano (plano de Argand-Gauss), o que permitiu a escrita de um número complexo na forma polar. Com isso, conseguiu-se calcular potências e raízes de modo eficiente e claro. Ainda no século XVIII, Gauss demonstrou o Teorema Fundamental da Álgebra.
Plano complexo:
O plano complexo, também chamado de plano de Argand-Gauss é uma representação geométrica do conjunto dos números complexos. Da mesma forma como a cada ponto da reta está associado um número real, o plano complexo associa biunivocamente o ponto ( x , y ) do plano ao número complexo x + yi. Esta associação conduz a pelo menos duas formas de representar um número complexo:- Forma retangular ou cartesiana:
- Forma polar:
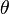 é o ângulo entre a semi-reta
é o ângulo entre a semi-reta 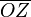 e o semi-eixo real, chamado de argumento do número complexo Z e denotado por
e o semi-eixo real, chamado de argumento do número complexo Z e denotado por  .
.Através da identidade
 , a forma polar é equivalente à chamada forma exponencial:
, a forma polar é equivalente à chamada forma exponencial: 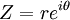
Operações elementares:
O conjunto dos números complexos é um corpo. Portanto, é fechado sobre as operações de adição e multiplicação, além de possuir a propriedade de que todo elemento não-nulo do conjunto possui um inverso multiplicativo. Todas as operações do corpo podem ser performadas através das propriedades associativa, comutativa e distributiva, levando em consideração a identidade
Sejam z e w dois números complexos dados por
 e
e  então definem-se as relações e operações elementares tal como segue:
então definem-se as relações e operações elementares tal como segue:- Identidade:
 se e somente se
se e somente se  e
e 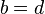 .
.
- Soma:
- Produto:
- Conjugado:
 , onde
, onde  denota o conjugado de z. Outra notação usada para o conjugado de z é z * .
denota o conjugado de z. Outra notação usada para o conjugado de z é z * .
- Produto de um Complexo por seu Conjugado:
 . Como i2 = − 1, temos que o produto de um Número Complexo a + bi pelo seu Conjugado a − bi se dá por:
. Como i2 = − 1, temos que o produto de um Número Complexo a + bi pelo seu Conjugado a − bi se dá por:  .
.
- Módulo:
- Inverso multiplicativo (para
 ):
):
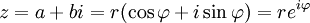 .
.
- Produto:
- Inverso multiplicativo (para
 ):
):
- Divisão:
- Potenciação:
- Conjugado:
O módulo:
Sejam z e w dois números complexos dados por e
e  , o módulo possui as seguintes propriedades:
, o módulo possui as seguintes propriedades:Propriedades algébricas:
O conjunto dos números complexos formam um corpo algebricamente fechado. Isso significa que toda equação algébrica de grau não nulo pode possuir como solução um número complexo. Mais formalmente, a seguinte equaçãoEste resultado é conhecido como teorema fundamental da álgebra e foi demonstrado primeiramente pelo matemático alemão Carl Friedrich Gauss. Uma consequência deste teorema é que todo polinômio de grau n pode ser decomposto em um produto de n fatores lineares complexos:
Radical algébrico
O radical algébrico é definido no conjunto dos números complexos como uma função multivalente, devido ao fato que a equação algébrica: , que são dadas pela fórmula de De Moivre:
, que são dadas pela fórmula de De Moivre: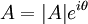 .
.Propriedades topológicas e analíticas
O conjunto dos números complexos munido da distância forma um espaço métrico completo. De fato, o módulo possui todas as características de uma norma.
forma um espaço métrico completo. De fato, o módulo possui todas as características de uma norma.Convergência nos complexos
Diz-se que uma sequência de números complexos é convergente se existe um número complexo
de números complexos é convergente se existe um número complexo 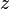 tal que:
tal que:- É fácil verificar que se
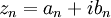 , então
, então  converge para
converge para 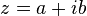 se e somente se
se e somente se 
 e
e  converge para
converge para 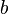 . converge para
. converge para - Do fato de que
 , é válido que se
, é válido que se  então
então 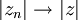
O conjunto dos números complexos como extensão algébrica
No campo da álgebra abstrata, o número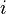 pode ser interpretado como o elemento que gera a extensão algébrica dos números reais contendo a raiz do polinômio
pode ser interpretado como o elemento que gera a extensão algébrica dos números reais contendo a raiz do polinômio  . Isto é, o corpo
. Isto é, o corpo  é isomorfo ao corpo quociente
é isomorfo ao corpo quociente  pela aplicação
pela aplicação  , homomorfismo de anéis tal que restrito aos reais é a aplicação identidade e que leva
, homomorfismo de anéis tal que restrito aos reais é a aplicação identidade e que leva 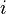 em
em  .
.Logaritmos
Função logarítmica natural
Definimos a função logarítmica natural de uma variável complexa z pela equação: =
=  +
+ 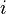 (
( 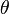 ±
±  )
)
 +
+ 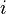
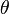
Função logarítmica decimal
Em termos de logaritmos decimais, podemos definir a função logarítmica anterior como:
 (
( 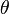 ±
±  )
)
![x = \sqrt[3]{-\frac{q}{2} + \sqrt{(\frac{q}{2})^2 +
(\frac{p}{3})^3}} + \sqrt[3]{- \frac{q}{2} - \sqrt{(\frac{q}{2})^2 +
(\frac{p}{3})^3}}.](http://upload.wikimedia.org/math/d/4/0/d40a53f0a19c385963fe4a7e455b725b.png)
![x=\sqrt[3]{2+\sqrt{-121}} + \sqrt[3]{2-\sqrt{-121}}](http://upload.wikimedia.org/math/7/d/5/7d5c0b00ec1dfa452318a220b4444549.png)
![x=\sqrt[3]{2+\sqrt{-121}} + \sqrt[3]{2-\sqrt{-121}} = (2 + \sqrt{-1}) + (2 - \sqrt{-1}) = 4](http://upload.wikimedia.org/math/4/9/e/49eaada2392d4bb6a501a76c68ff1a6c.png)




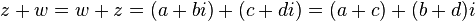



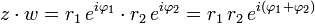
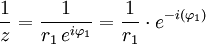
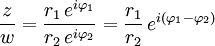


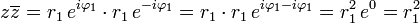

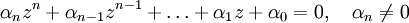





Nenhum comentário:
Postar um comentário